シェーダーのロジックは特別であり、JavaScriptやその他のプログラミング言語で慣れているものとは異なります。構文は似ていますが、ロジックの実装方法が異なります。 ある種のブラックボックスのようなもので、データを入力すると、フラグメントシェーダーには色が出力され、頂点シェーダーには位置が出力されます。

しかし、出力をどのようにコントロールするのでしょうか？どのようにして思い通りの見た目にするのでしょうか？ここでシェーピング関数の出番です。

このレッスンではフラグメントシェーダーに焦点を当てますが、同じ原則が頂点シェーダーにも適用されます。

実践ゾーン

シェーピングの技をマスターするには、練習と実験が必要です。シェーダーの動作に慣れるまでには時間がかかりますが、一度コツを掴めば素晴らしい効果を生み出すことができるようになります。

成功のための最善の環境を提供するために、この3Dアートギャラリーシーンを用意しました。これでリアルタイムでシェーダーを視覚化することができます。

クリエイティビティが湧いてきませんか？これらの空のフレームはあなたの傑作を待っています！

使用された3Dモデルは、Maxim MavrichevによるVR Galleryで、Creative Commons Attributionのライセンスの下で提供されています。

ギャラリー内をナビゲートするために、<CameraControls />を使用して一人称視点のカメラを作成し、テクスチャのサイズを減らすためにSquooshを使用しました。

SimpleShaderMaterial

ギャラリー内のすべてのフレームはSimpleShaderMaterialのコピーであり、これは次のような基本的なカスタムシェーダーです：

• uColor: 色
• uTime: アプリケーション開始からの経過時間
• vUv: フラグメントのUV座標（両軸で0から1）

これらはすべて<App.jsx />内で拡張され、シーン内で宣言的に使用できるようになっています。

これらはギャラリー内の位置に基づいて名前が付けられていますが、傑作を作成したらもっと意味のある名前に自由に変更してください！

Functions

私たちのシェーダーの各フラグメントに対して、異なる入力で同じコードが実行されます。

ラインを描画したい場合、if文を使用してピクセルがラインの内側かどうかをチェックすることができます。しかし、より複雑な形状を描くのは非常に困難で非効率的です。

その代わりに、関数を使用して出力を形作ります。心配しないでください。関数を使用するために数学の専門家である必要はありません。利用可能な関数とその働きを理解するだけで十分です。

関数を、入力を受け取り、出力を与える機械と考えてください。例えば、関数 f(x) = x * 2 は数値 x を受け取り、その結果として x * 2 を与えます。

異なる関数の効果を視覚化するために、Graphtoyを使用します。これは関数を入力してその出力を見るための簡単なツールです。このツールを使用すると、シェーダーで関数を実験する際にその理解を検証するのに役立ちます。

Graphtoyで f(x) = x * 2 関数を視覚化しましょう：

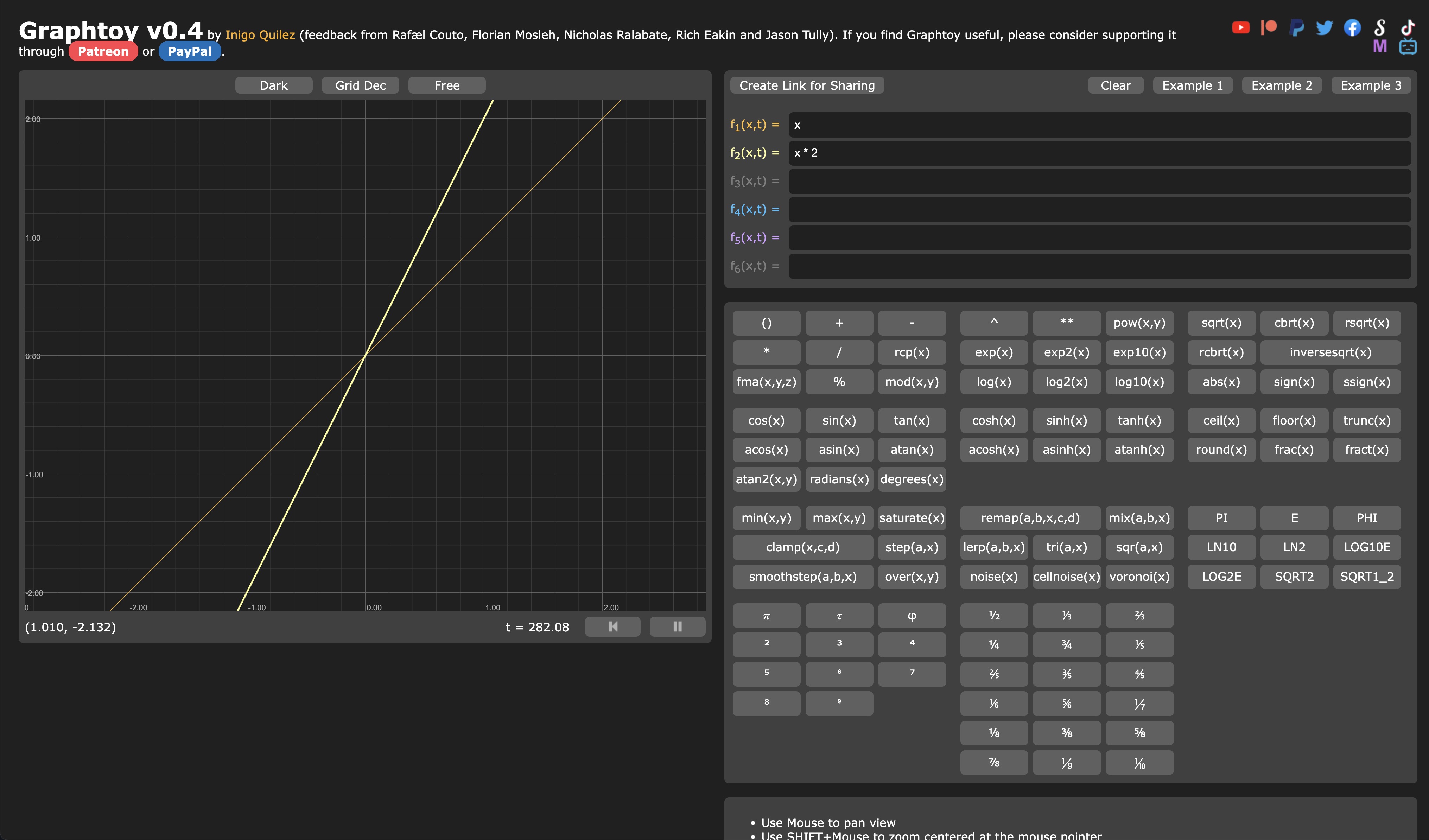
シェーダーを実験する際に、Graphtoyはあなたの親友になるでしょう。

利用可能な異なる関数で実験を始めましょう。

Step

step関数は、入力がしきい値を下回ると 0 を返し、しきい値を上回ると 1 を返すシンプルな関数です。

この関数は二つのパラメータを取ります：

• edge: しきい値
• x: 入力値

フロントフレーム ArtFront02Material.jsx フラグメントシェーダーで試してみましょう：

Copy
void main() {
  float pct = 1.0;
  pct = step(0.5, vUv.x);
  vec3 finalColor = pct * uColor;
  gl_FragColor = vec4(finalColor, 1.0);
}

色を表示する割合を決定する変数 pct を宣言します。これをデフォルトで 1.0 に設定し、step 関数を使用して vUv.x が 0.5 未満の場合 0.0 に設定します。

フレームの左半分が黒く、右半分が uColor ユニフォームで設定された色になるのがわかります。

異なるしきい値で垂直軸に適用してみましょう：

Copy
void main() {
  float pct = 1.0;
  pct = step(0.2, vUv.y);
  vec3 finalColor = pct * uColor;
  gl_FragColor = vec4(finalColor, 1.0);
}

フレームの下部20%が黒で、残りが紫であるのがわかります。

UV座標の原点はフレームの左下隅にあり、[0, 0] が左下隅、[1, 1] が右上隅です。

効果を反転させたい場合は、単に step 関数のパラメータを入れ替えるだけです：

Copy
void main() {
  float pct = 1.0;
  pct = step(vUv.y, 0.2);
  vec3 finalColor = pct * uColor;
  gl_FragColor = vec4(finalColor, 1.0);
}

今度は逆の効果が得られます。

Mix

The mix function は、2つの値の間の線形補間を返すシンプルな関数です。

3つのパラメータを取ります:

• x: 最初の値
• y: 2番目の値
• a: x と y の間を補間する値

試してみましょう：

Copy
void main() {
  float pct = 1.0;
  pct = mix(0.0, 1.0, vUv.x);
  vec3 finalColor = pct * uColor;
  gl_FragColor = vec4(finalColor, 1.0);
}

黒から紫の美しいグラデーションが見えます。

他の多くの関数と同様に、ベクトル成分などの他のタイプのデータで使用することもできます。垂直軸に白から紫へのグラデーションを作成してみましょう：

Copy
void main() {
  vec3 whiteColor = vec3(1.0);
  vec3 finalColor = mix(whiteColor, uColor, vUv.y);
  gl_FragColor = vec4(finalColor, 1.0);
}

白から紫の美しいグラデーションが見えます。

mix 関数を最初に呼び出して pct 値を取得し、それを使って whiteColor と uColor の間を補間することで、補間値を変更してみましょう：

Copy
void main() {
  vec3 whiteColor = vec3(1.0);
  float pct = mix(0.0, 0.3, vUv.y);
  vec3 finalColor = mix(whiteColor, uColor, pct);
  gl_FragColor = vec4(finalColor, 1.0);
}

pct の最大値が 0.3 なので紫がとても淡いです。

Graphtoy を使って、mix 関数を試し、その動作を理解してください。

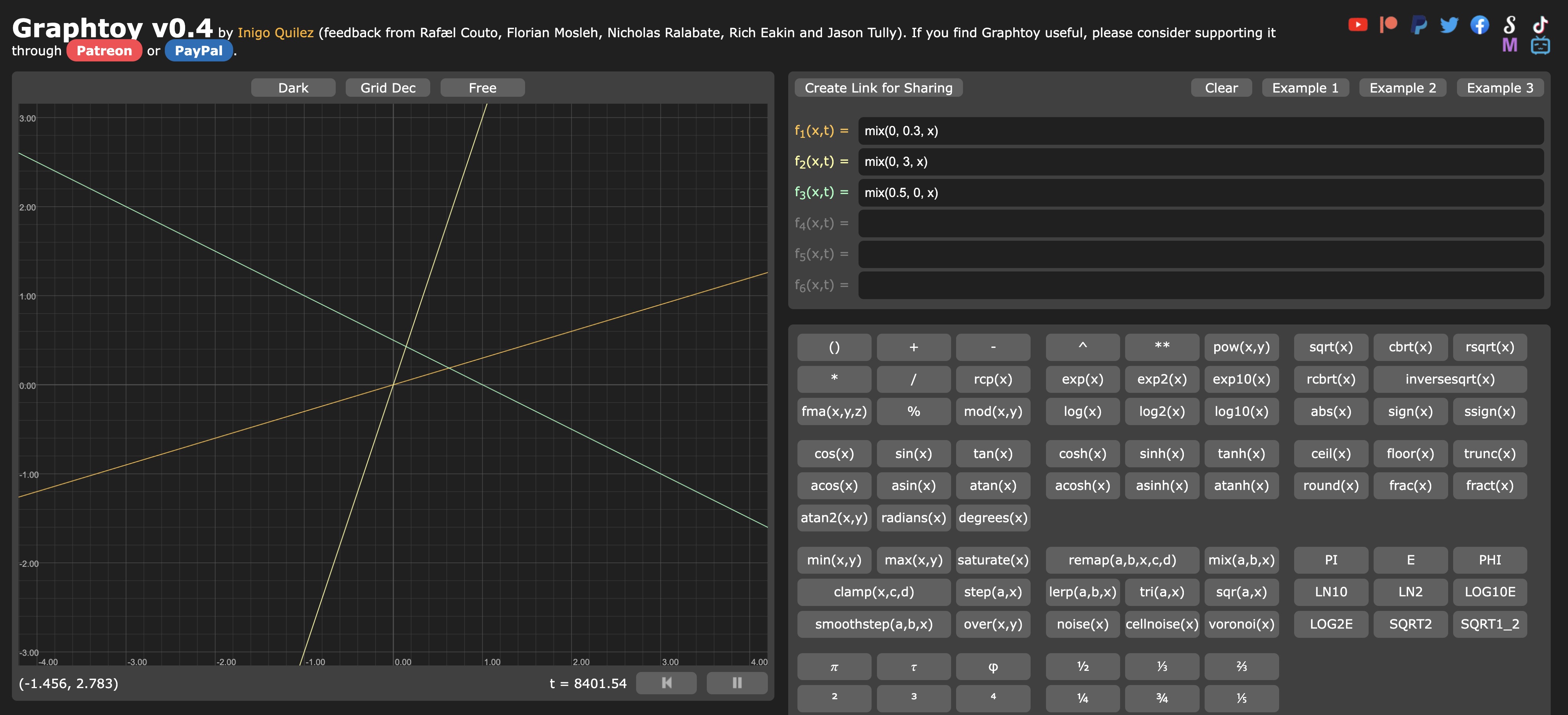
mix 関数を使用した3つの異なる補間は、全く異なる結果をもたらします。

Smoothstep

smoothstep関数は、2つの値の間でスムーズな補間を返すシンプルな関数です。

この関数は3つのパラメータを取ります:

• edge0: 下限値
• edge1: 上限値
• x: edge0とedge1の間を補間する値

この関数は3つの異なる結果を返します:

• xがedge0より小さい場合は0.0
• xがedge1より大きい場合は1.0
• xがedge0とedge1の間にある場合は0.0から1.0の間のスムーズな補間

pct値を変更するために使ってみましょう:

Copy
void main() {
  vec3 whiteColor = vec3(1.0);
  float pct = smoothstep(0.4, 0.6, vUv.y);
  vec3 finalColor = mix(whiteColor, uColor, pct);
  gl_FragColor = vec4(finalColor, 1.0);
}

遷移は0.4から0.6の間のみです。それ以下はすべて白色、それ以上はすべて紫色になります。

Min & Max

min と max は、2つの入力値の間で最小または最大の値を返すシンプルな関数です。これらはJavaScriptの Math.min と Math.max 関数と同じように動作します。

これらを使って pct 値を微調整してみましょう。まず、 pct が常に 0.4 より小さくならないようにします（つまり、完全に白くならないようにします）:

Copy
void main() {
  vec3 whiteColor = vec3(1.0);
  float pct = smoothstep(0.4, 0.6, vUv.y);
  pct = max(pct, 0.4);
  vec3 finalColor = mix(whiteColor, uColor, pct);
  gl_FragColor = vec4(finalColor, 1.0);
}

次に、 pct が常に 0.6 より大きくならないようにします（つまり、完全に紫にならないようにします）:

Copy
void main() {
  vec3 whiteColor = vec3(1.0);
  float pct = smoothstep(0.4, 0.6, vUv.y);
  pct = max(pct, 0.4);
  pct = min(pct, 0.6);
  vec3 finalColor = mix(whiteColor, uColor, pct);
  gl_FragColor = vec4(finalColor, 1.0);
}

色が洗い出されており、非常にスムーズなトランジションが見られます。

Graphtoyで可視化してみましょう:

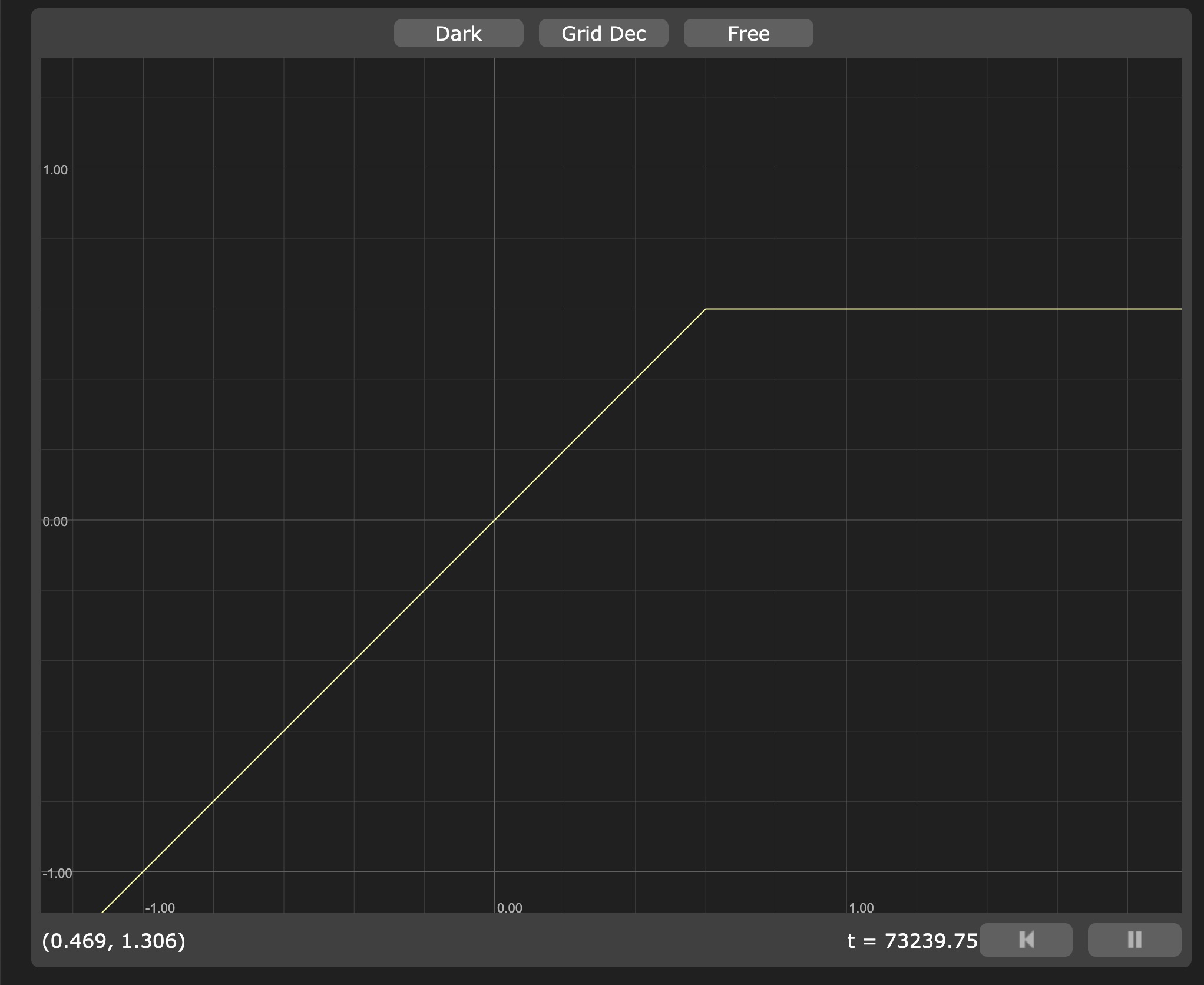
max(x, 0.4) の表現

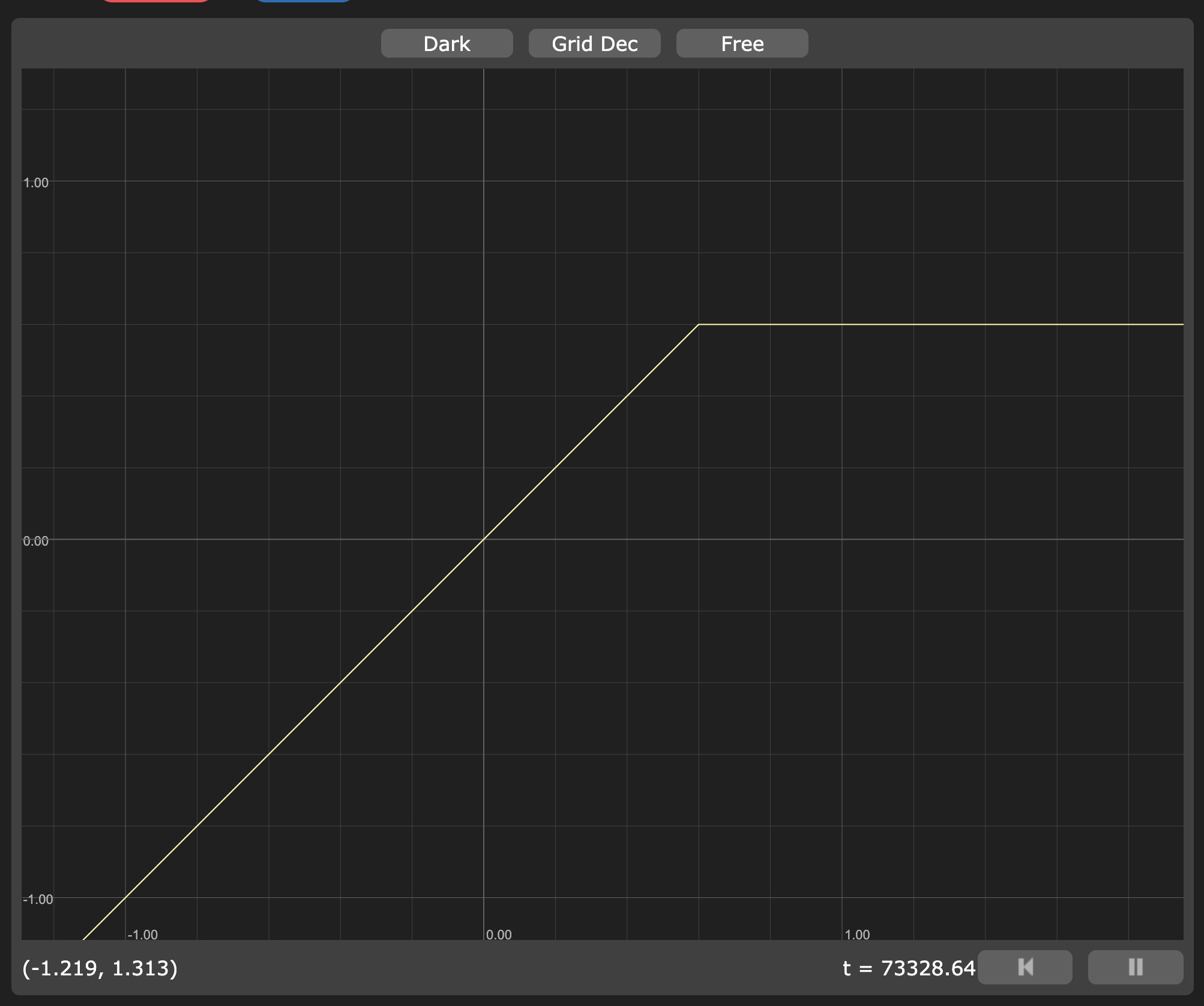
min(x, 0.6) の表現

そして、これらを組み合わせると:

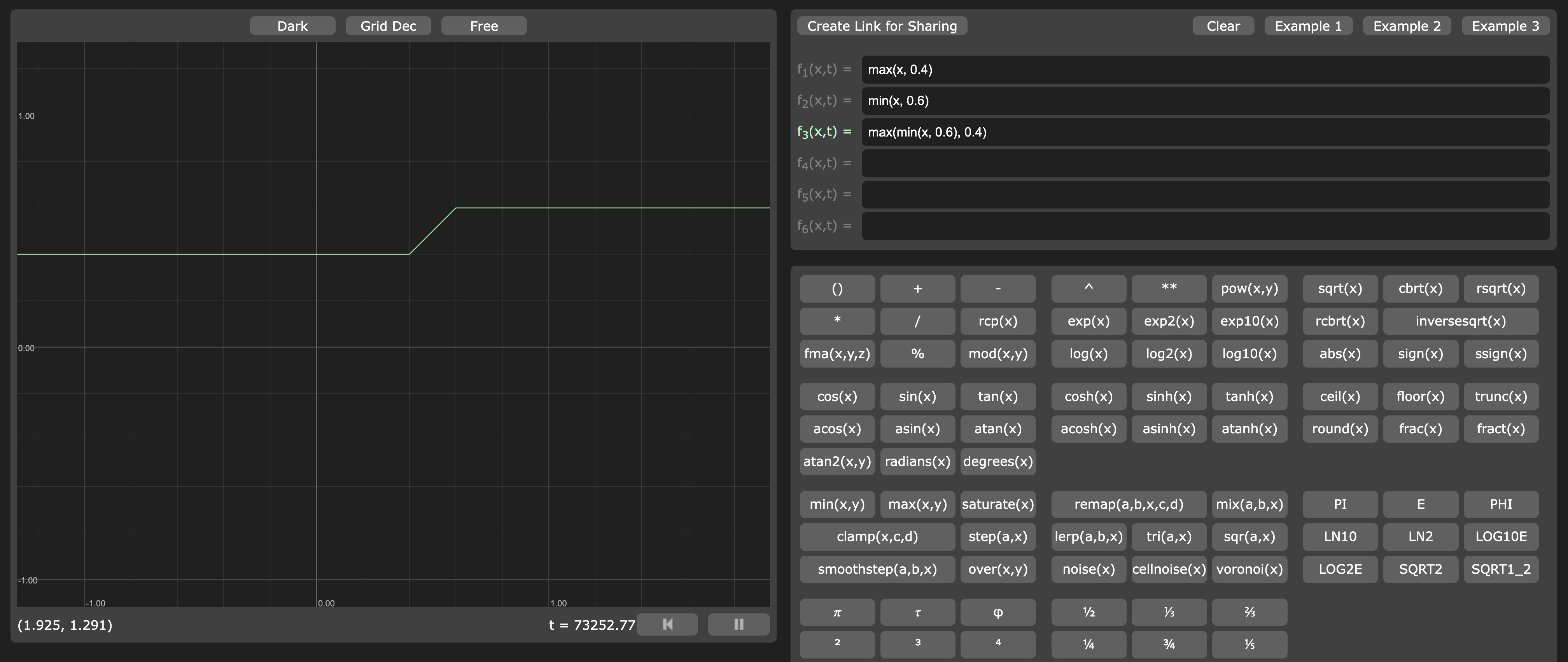
値が 0.4 未満に下がらず、 0.6 を超えないことがわかります。

min と max 関数の組み合わせは、clamp 関数で置き換えられます。これは、 min(max(x, min), max) の略記です。

Operations & patterns

Before we discover many other useful functions, let's see how we can use operations to create patterns.